| 名称 | 円柱形つまみの回転操作の開始時の指の使用状況データ |
|---|---|
| 計測年 | 1997年 |
| 計測場所 | 千葉県 |
| 計測対象者 | 19-20歳の日本人男女32人 |
| 計測項目 | 円柱形つまみの回転操作の開始時に使用される指の本数と接触位置 |
| 特徴 |
人は、円柱形の器具を操作する際、視覚と触覚により対象物の大きさ・形状・材質・トルク等を判断し、特に意識することなく使用する指の本数を変えて対応している。 |
| その他 | ご利用にあたっての注意事項(Read me)を確認の上、ご利用ください。 |
■計測目的
回転操作を必要とする日常生活における各種操作機器を想定し、操作開始時に使用される指の本数と接触位置の直径変化による推移を確認する。
■計測装置
- 台:幅600mm奥行き450mm高さ800mm
上面に300mm四方のアクリル板をはめ、その中央に回転軸を立てる。 - 円形つまみ:木製の円柱47種類
高さは50mmで共通。直径は7mm~130mmの間で平均3mm間隔
台の回転軸に円形つまみを1つずつはめ込む。回転負荷は掛けない(トルク:微小。450cmg以下)。 - 撮影装置:デジタルビデオカメラ
台の下に、垂直上向きに設置した。 - 握力計測:握力計
- 摘み力計測:ピンチメーター
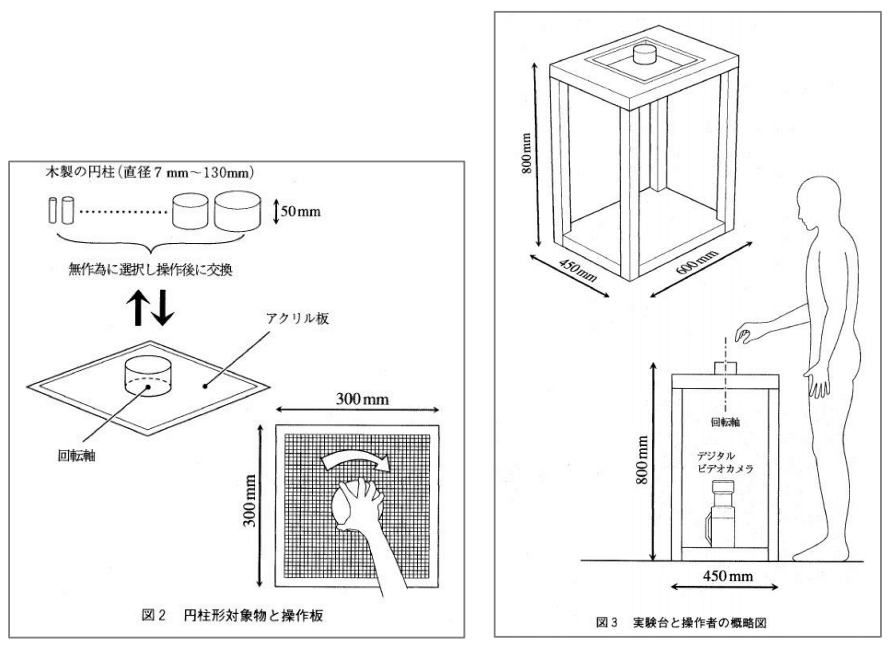
図1 計測装置
(「円柱形つまみの回転操作における指の使用状況について」1)より引用)
■計測方法
- 円形つまみを1つずつ台に取り付ける。つまみの使用順序はランダムとする。
- 被験者は台の前に立つ。立ち位置、立ち方は制限しない。
- 被験者に、「右手でつまみ、右に回してください。」と指示する。被験者はその指示をもとに右手で円形つまみをつまみ、右に回した。操作の状況を真下に設置したビデオ撮影した。
- 130mmより大きなものについては、つかむことができる最大のものを実際に選択してもらい、その直径を確認した。
- 最後に、被験者はアクリル板の上に右手を広げて置いた。その状態をビデオ撮影した。
- 得られた画像から、各指と円柱の接触状況を読みとった。円柱断面の中心を原点(0.0)として、下方から見た画面上の縦軸をy、横軸をxとして各プロット位置をxy座標系で読み取った。読み取った結果をもとに、指の使用本数を確認した。
- また、右手を広げた画像から各部位の寸法を計測した。
■計測結果
1.被験者について
- 計測人数:19-20歳の男性23人、女性9人、計32人
- 利き手:全員右利き
- 身体特性:身長、手長、手幅、第1指~第5指長、握力、つまみ力(第1指と第2指、第1指と第3指、第1指と第4指、第1指と第5指)の平均値と標準偏差は表1の通りであった。結果からこの実験における被験者の手の寸法・握力・摘み力等は、特に際立った特性を持っておらず、平均的な19~20歳の男女のサンプルであったと判断した。
表1 被験者の身体特性
(出典:「円柱形つまみの回転操作における指の使用状況について1)」)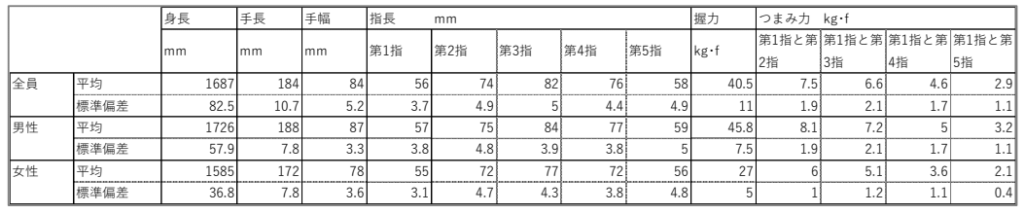
2.データが得られた円形つまみの直径について
下記の45種類の直径のつまみについて、データが得られた。
表2 データが得られた円形つまみの直径(mm)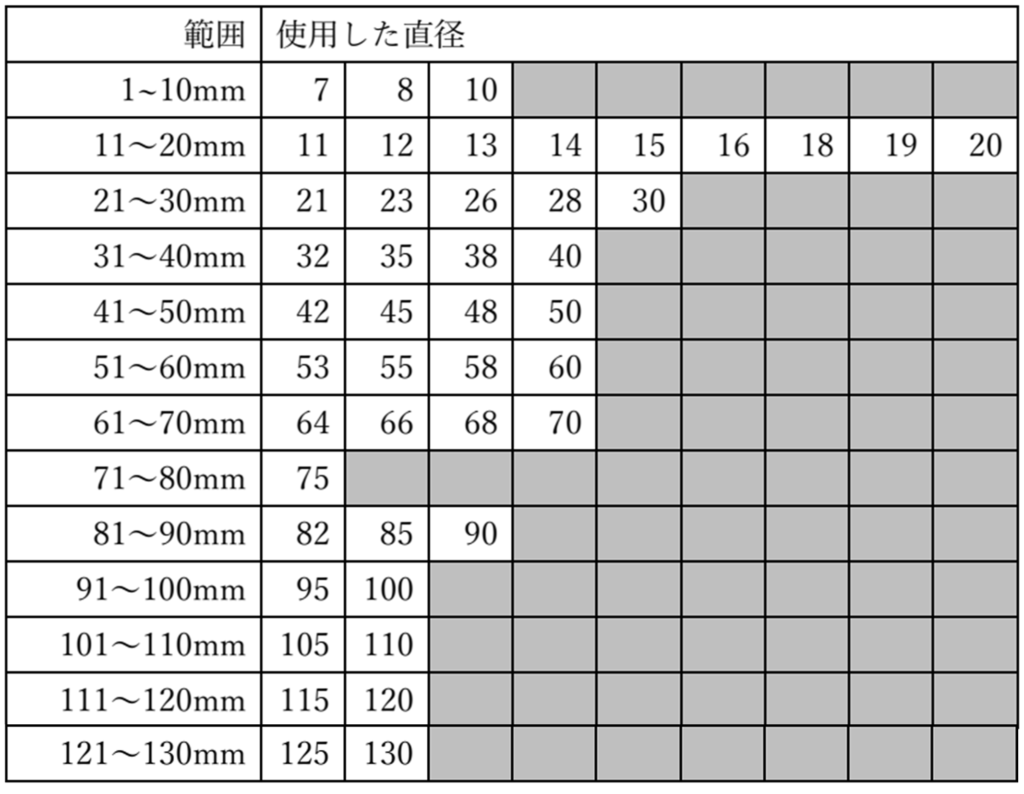
3.回転操作開始時に使用する指の本数が変化する境界値について
直径ごとに使用された指の本数を確認し、各被験者について散布図を作成すると、図2のように表すことができる。多くの場合、図2の図5-1のように操作開始時の指の本数の境界値が明確に現れているが、中には例外的なものも見られた。 図5-2は、2・3・4本の境界が曖昧で、直径32mm以降は全て5本の指が使われている。図5-3は、2本と3本、3本と4本の境界がはっきりしているものの、4本と5本の境界値を特定することは難しい。図5-4では、3本と4本の境界は確認できるが、2本と3本、4本と5本の場合が交錯しており、境界値を確定することはできない。 全体の傾向は、図5-5のとおりである。実際は、指の本数が小数値をとることは有り得ないが、平均値を散布図で示すことで変化の推移を流れとして把握することができる。 4本使用から5本使用にかけての流れは、傾斜が緩やかで、範囲としても広く続いている。このことから4本使用と5本使用の境界となる円柱の直径は、 個人差が大きく、また、回転操作開始時における第4指と第5指の役割は、直径の増大に伴い徐々に増していくとも解釈できる。
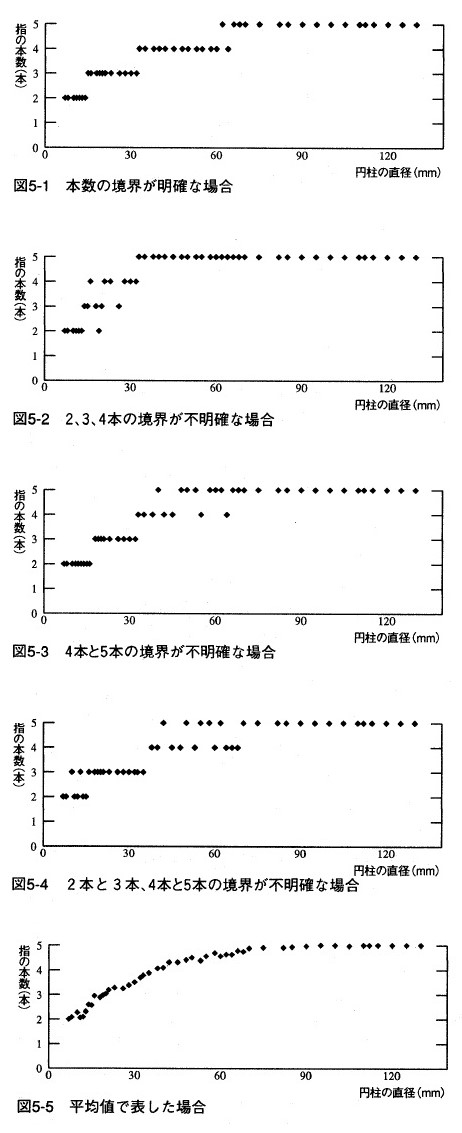 図2 円柱の直径と使用される指の本数との関係
図2 円柱の直径と使用される指の本数との関係
(「円柱形つまみの回転操作における指の使用状況について」1)より引用)
被験者全体の人数による相対的な使用本数の推移は図3で表され、この図から任意の直径に対する指の使用本数を推定することができる。図3に描かれたそれぞれの曲線で、被験者の半数がその本数で操作を開始している相対度数50%付近を境界とし、隣り合う曲線との交点も参考にすると、指の使用本数が変化する直径の境界値は、 表3のように推定できる。
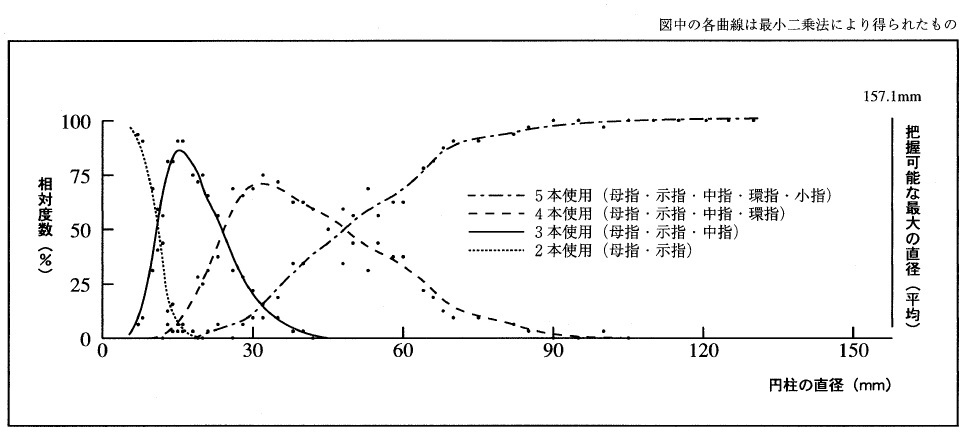 図3 回転操作開始時に使用される指の本数の推移
図3 回転操作開始時に使用される指の本数の推移
(「円柱形つまみの回転操作における指の使用状況について」1)より引用)
表3 指の使用本数が変化する直径の境界値
(「円柱形つまみの回転操作における指の使用状況について」1)より引用)
| 指の本数 | 直径 |
| 2本→3本 | 10mm~11mm |
| 3本→4本 | 23mm~26mm |
| 4本→5本 | 45mm~50mm |
直径10mm~11mmのつまみは、2本使用される場合と3本使用される場合が半数ずつであるが、これより小さくなる程、2本で摘む割合が高くなる。同様に、45mm~50mmのものは4本使用と5本使用が半数ずつで、それ以上のものは徐々に5本使用の割合が高くなり、90mm以上では、ほぼ全員が5本の指全てを使用するようになった。
把握可能な最大の直径を男女合わせて平均した結果、157.1mmで、標準偏差は10.2mmであった。当然のことながら、この値より大きな直径の回転操作機器・つまみは、一般的な道具の範囲を超えるものである。
4.直径の変化による各指の接触位置の推移について
回転操作に必ず使用される第1指(母指)を縦軸に整列させるように、全座標値を変換したのち、接触位置の平均と標準偏差を算出した。(なお、生データは、手の下から(手のひら側)から得た座標値である。)
図4は、全被験者の平均と標準偏差から推移の傾向と分布の幅を表したものである。(なお、図4は、円形つまみを上からつまんでいる状態を理解しやすくするため、データの左右を反転させて手の上から(手の甲側から)見た図とした。)図中に記したとおり、第1指をy軸上に揃えて基準とした場合、他の4指の推移はxyを変数とした二次曲線で近似することができる[注11]。平均値は、プロット結果をxy座標で読みとった後、各直径の円上の点として極座標(θ,r)変換し、算出されたものである[注12]
第1指を直線上に揃えた図4で、他の4指が曲線的に推移するのは、各直径に対応したつかむ動作における母指の関節の自由度に起因すると考えられる。母指の自由度は5で、他の4指よりも1多い[注13]。つまり、図4に示した各曲線の特徴は、被験者の指の長さと母指の可動特性によるところが大きいと考えられる。今回の実験ではトルクを微小なものとし、回転操作開始時の接触状態を重視したが、第4指(環指)と第5指(小指)が尺骨側の前腕の筋肉を利用して、より強い力での把握を助けることを考えれば、直径とトルクの組み合わせによって実験を行う価値もある。また、性別による差は特に見られなかった。
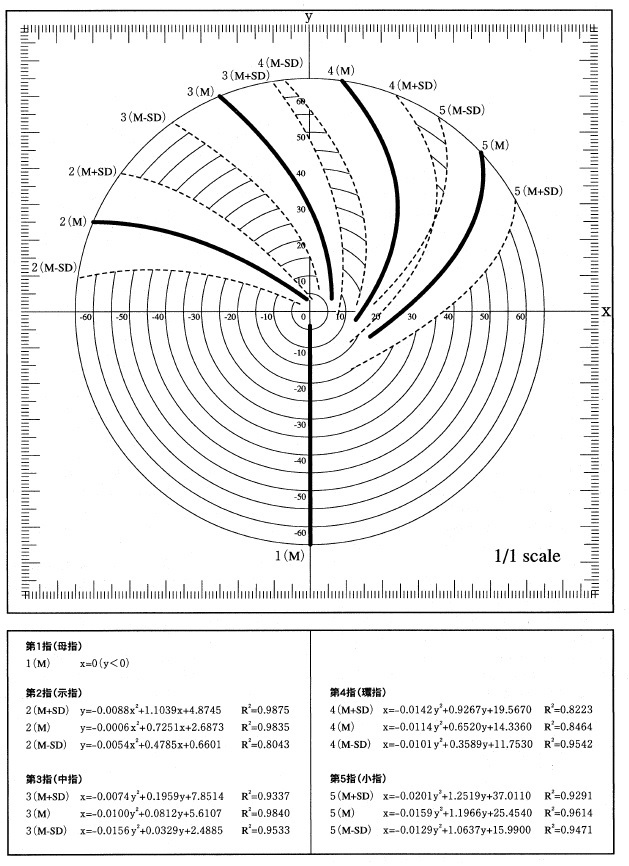 図4 回転操作開始時における円柱と各指の接触位置の推移(母指を軸上に揃えた場合)
図4 回転操作開始時における円柱と各指の接触位置の推移(母指を軸上に揃えた場合)
(「円柱形つまみの回転操作における指の使用状況について」1)より引用)
注
11) 通常のxy座標による関数表示では、yを従属変数とし、y・f(x)という形をとる方が一般的だが、ここでは、複雑になることが予想される無理関数による表記を避けるため、x=f(y)の形で二次関数として表している。 しかし、第2指に限っては、その曲線の特性から、xを従属変数、yを独立変数とした方が表記し易く、二次方程式として解釈し易いため、y=f(x)の形式で表している。
12) プロットした結果をxy座標ではなく、極座標として扱うことで円弧上に平均値を得ることができる(図5)。ただし、極座標上で平均・標準偏差を三角関数を用いて算出する場合、θの値が0°、90°、180°、270°を境界とする前後で、符号±の変化に注意しなければならない。
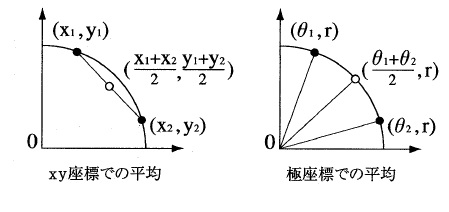 図5 xy座標と極座標
図5 xy座標と極座標
13) 手指の関節の自由度の出典:
雨宮俊彦:手指技能研究の枠組みについて,人間工学,24,6,353-361,1988
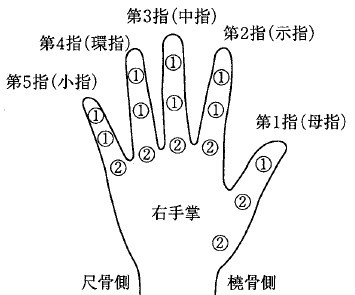
図6 手指の関節の自由度
(○の中の数字は各関節の自由度を表している。)
5.まとめ
今回の操作実験によって得られた結果は、製品デザインの立場から、回転操作機器の断面形状の凹凸を設計するのに役立つものである。具体的には、使用される指の本数と接触位置のデータを、操作開始時点に絞って、直径との関係でまとめたものであるが、直径の変化による指の使用本数の境界値を推測できただけでなく、接触位置の推移を二次関数の方程式として近似することができた。
参考文献
1)松崎元,大内一雄,上原勝,上野義雪,井村五郎:円柱形つまみの回転操作における指の使用状況について,デザイン学研究,Vol.45No.5,pp69-76,1999
![一般社団法人 人間生活工学研究センター [ HQL ] データベースサイト ロゴ](https://www.hql.jp/database/wp-content/uploads/hqldatabase_logo.png)
![一般社団法人 人間生活工学研究センター [ HQL ] データベースサイト ロゴ](https://www.hql.jp/database/wp-content/uploads/hqldatabase_logo_Sticky.png)